Video: Kakav je odnos između površine i zapremine kocke?
2024 Autor: Miles Stephen | [email protected]. Zadnja izmjena: 2023-12-15 23:34
Za kocke manji od ovoga, površina je veći u odnosu na volumen nego što je u većem kocke (gde volumen je veći u odnosu na površina ). jasno ilustruje da kako se veličina objekta povećava (bez promjene oblika), ovaj omjer se smanjuje.
Isto tako, ljudi se pitaju kakav je odnos između površine i zapremine?
The površina prema zapremini omjer objekta je odnos između dva merenja. To je omjer Površina prema zapremini . To pokazuje poređenje između veličina vanjskog dijela objekta i količina unutra. Mali ili tanki predmeti imaju veliki površina uporedio to the volumen.
Nadalje, da li je površina ista kao i zapremina? Površina je zbir od oblasti svih lica čvrste figure. Mjeri se u kvadratnim jedinicama. Volume je broj kubnih jedinica koje čine čvrstu figuru.
Zbog toga, da li su površina i zapremina kocke iste?
Znamo da je zapremine kocke je jednako s3, gdje je s dužina date stranice kocka . Budući da su strane a kocka su sve isto , the površina of the kocka je jednako 6 puta području jednog lica.
Kakav je odnos između površine i volumena i vremena difuzije?
Kada se ćelija poveća u veličini, volumen raste brže od površina , jer volumen je kockasto gdje površina je na kvadrat. Kada ima više volumen i manje površina , difuzija traje duže i manje je efikasan.
Preporučuje se:
Kakav je promjenjivi odnos između volumena i površine kako se objekt povećava?
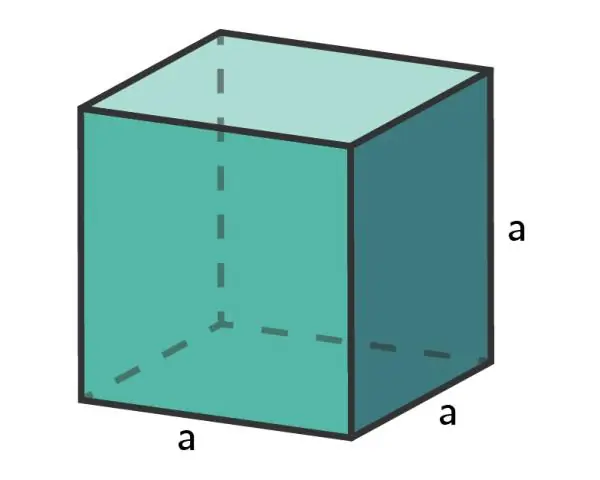
Kako se veličina kocke povećava ili ćelija postaje veća, tada se omjer površine i volumena - SA:V omjer smanjuje. Kada je objekat/ćelija vrlo mali, ima veliki odnos površine i zapremine, dok veliki objekat/ćelija ima mali odnos površine i zapremine
Koja je razlika između površine i bočne površine?
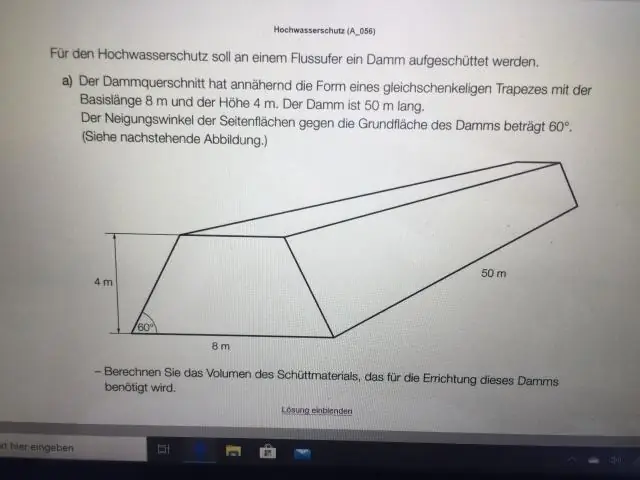
Bočna površina je površina svih strana isključujući površinu baze. Ukupna površina bilo kojeg čvrstog tijela je zbir površina svih površina tijela
Kakav je odnos između površine i zapremine kugle?
Za sferu, površina je S= 4*Pi*R*R, gdje je R poluprečnik sfere, a Pi je 3,1415 Volumen sfere je V= 4*Pi*R*R*R/3. Dakle, za sferu, odnos površine i zapremine je dat sa: S/V = 3/R
Zašto je važan odnos površine i zapremine?
Odnos površine i zapremine je važan jer, kako ćelija stari i proizvodi esencijalne proizvode kao što su proteini, ona se povećava u veličini. Ćelija postaje sve veća, pa je i njen volumen sve veći, ali nažalost za razliku od volumena, površina ćelije se ne povećava tako brzo
Kakav je odnos između masene gustine i zapremine?
Masa je koliko je nešto teško, zapremina vam govori koliko je velika, a gustina je masa podijeljena sa zapreminom